[C++] 백준 10844번 - 쉬운 계단 수

---

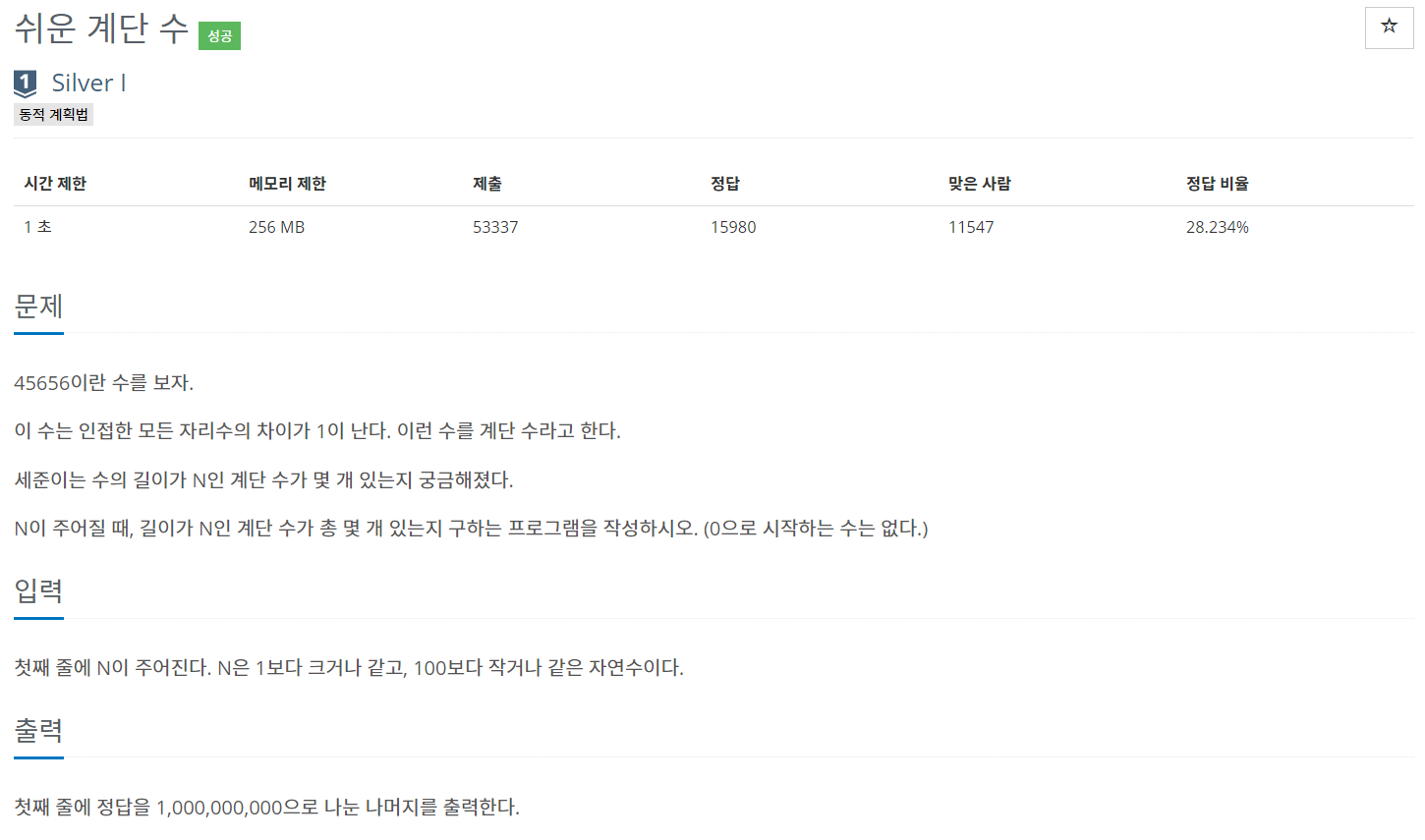
0. 문제

 

https://www.acmicpc.net/problem/10844

 

1. 아이디어

 

N=1 → 1, 2, 3, 4, 5, 6, 7, 8, 9
N=2 → 10, 12, 21, 23, 32, 34, 43, 45, 54, 56, 65, 67, 76, 78, 87, 89, 98

1)  이처럼 수의 길이가 N일 때 계단수는, 길이가 N-1인 계단수에 일의 자리 +-1을 붙여주면 된다.

 

2) 이때, 일의 자리가 0과 9로 끝나는 경우를 체킹해줘야한다. 0이면 1만 가능! 9이면 8만 가능! 나머진 각각 두 개씩.

 

3) 점화식으로 표현하면 dp[N][L] = dp[N-1][L-1] + dp[N-1][L+1] (0<N<9) 로 표현 가능하다.

 

2. 소스코드

 

#include <iostream>
#define MOD 1000000000
int main()
{
    int N, sum = 0;
    std::cin >> N;
 
    int dp[101][10] = { 0, }; // dp[N][L]에서 N은 길이, L은 자리수
 
    for (int i = 1; i < 10; i++)
        dp[1][i] = 1;
 
    for (int i = 2; i <= N; i++)
    {
        dp[i][0] = dp[i - 1][1] % MOD;
        for (int j = 1; j < 9; j++)
            dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j + 1]) % MOD;
        dp[i][9] = dp[i - 1][8] % MOD;
    }
 
    for (int i = 0; i < 10; i++)
        sum = (sum + dp[N][i]) % MOD;
 
    std::cout << sum % MOD;
}

 

3. 결과

 

 

4. 피드백

 

• 이차원배열도 잘 활용.. 배운 개념들을 종합적으로 잘 활용하자.
• 오버플로우 조심!

---