| 0. 문제 |
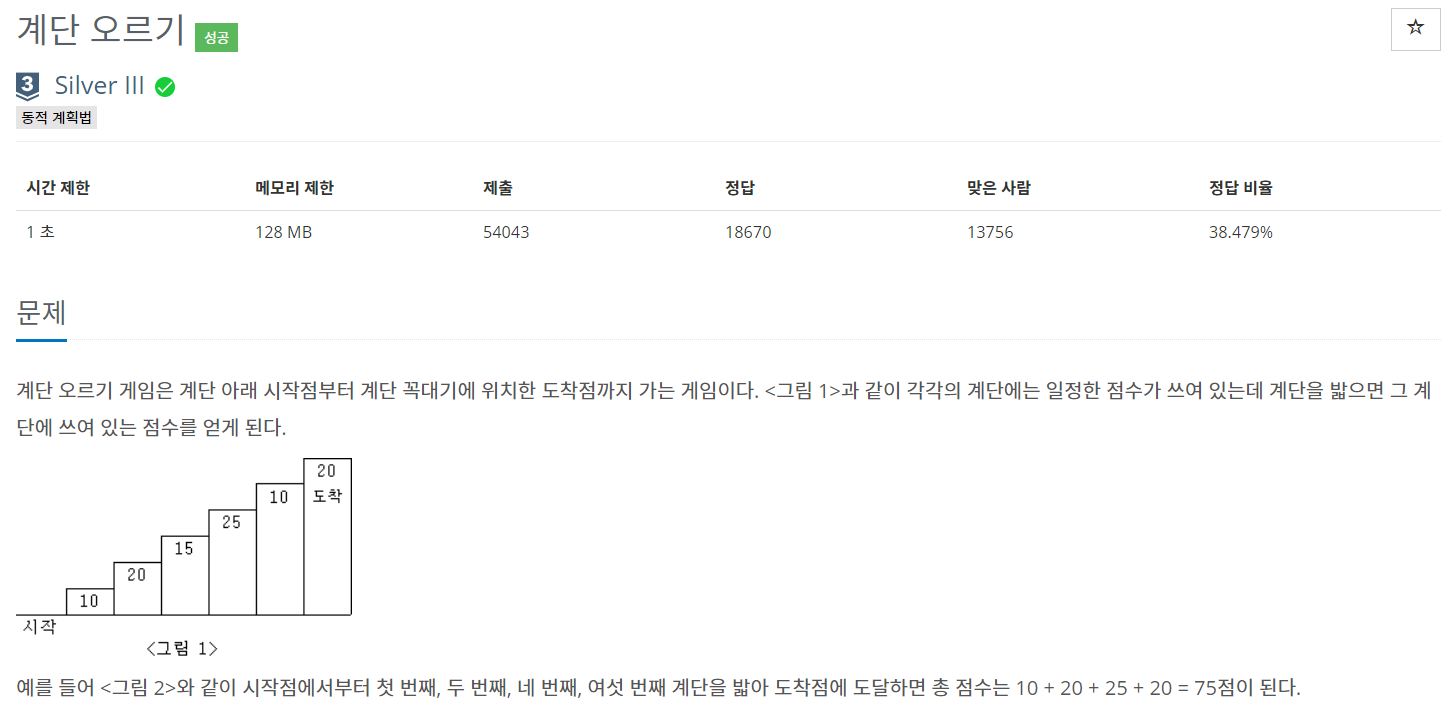
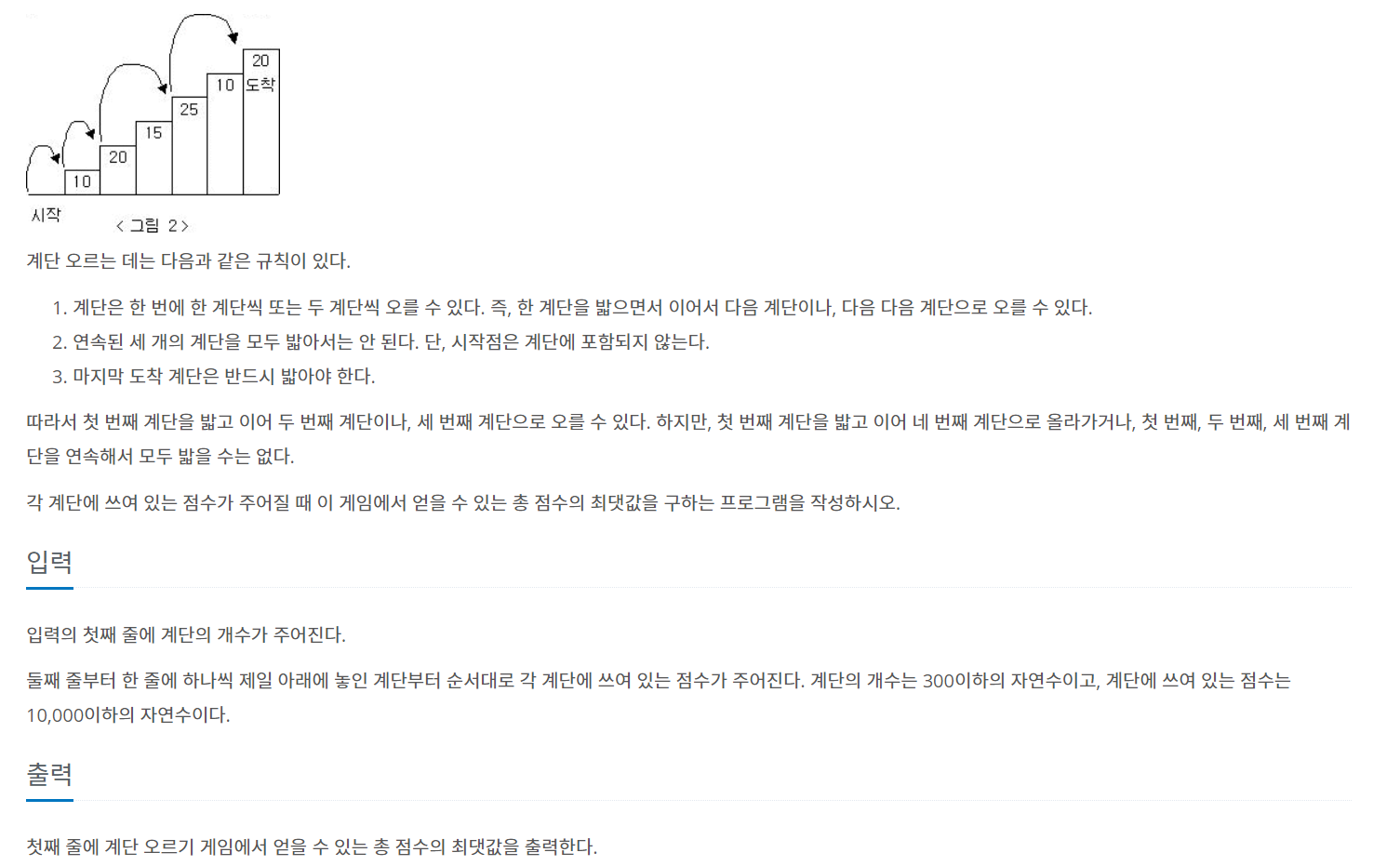
| 1. 아이디어 |
1) 하..
2) 우선 마지막 계단을 반드시 밟을 수 있게 점화식을 세웠을 때
| 밟는다 | 밟지 않는다 | 밟는다 | 밟는다 |
| ???? | 밟는다 | 밟지 않는다 | 밟는다 |
위와 같은 두가지 경우가 성립한다!
일단 지금 세운 점화식을 이용해서 dp의 값들을 구하기 위해선 최소 3개의 값들이 필요하며 dp[0], dp[1], d[2]는 손쉽게 구할 수 있다. (따라서 반복문은 i = 3부터)
3) max 함수를 통해 위에서 세운 두가지 경우 중 더 큰 값을 가지는 경우를 선택하면 된다!
4) 각 점화식에 필요한 부분 이전은, 어떤 계단들을 밟던지 아무 상관이 없다. 따라서 그냥 최댓값을 저장해둔 dp값을 이용하기만 하면 된다!!
| 2. 소스코드 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#include <iostream>
#include <algorithm>
int arr[300], dp[300], N;
int main()
{
std::cin >> N;
for (int i = 0; i < N; i++)
{
std::cin >> arr[i];
dp[i] = -1;
}
dp[0] = arr[0];
dp[1] = std::max(arr[0] + arr[1], arr[1]);
dp[2] = std::max(arr[0] + arr[2], arr[1] + arr[2]);
for (int i = 3; i < N; i++)
{
dp[i] = std::max(dp[i - 3] + arr[i - 1] + arr[i], dp[i - 2] + arr[i]);
}
std::cout << dp[N - 1];
}
|
cs |
| 3. 결과 |

| 4. 피드백 |
-
재귀함수가 코드의 흐름을 보기가 더 쉽다던데 나는 봐도 봐도 어렵다..
-
top-down 이니 bottop-up 이니 굳이 연연하지 말고 더 답을 내기 편한 방법을 따르자!
-
dp는 먼저 점화식을 세워야 한다!!! 그래야 답을 구하기가 편리하다.
'알고리즘 > BOJ' 카테고리의 다른 글
| [C++] 백준 9461번 - 파도반 수열 (0) | 2020.03.25 |
|---|---|
| [C++] 백준 1699번 - 제곱수의 합 (0) | 2020.03.23 |
| [C++] 백준 1912번 - 연속합 (0) | 2020.03.23 |
| [C++] 백준 11054번 - 가장 긴 바이토닉 부분 수열 (0) | 2020.03.22 |
| [C++] 백준 11722번 - 가장 긴 감소하는 부분 수열 (0) | 2020.03.22 |



